Como calcular média ponderada no Excel
Como calcular média ponderada no Excel
Diferentemente da média aritmética, a média ponderada leva em consideração o peso referente a cada um dos valores. Dessa forma, o resultado depende não apenas de uma média simples entre os valores, mas de uma média que leva em consideração a relevância de determinados valores em relação aos demais. Para calcular a média ponderada no Excel, você precisa de duas funções: SOMA e SOMARPRODUTO.
Versão em vídeo
Download dos arquivos
Você pode baixar os arquivos utilizados no tutorial em vídeo. O arquivo inicial refere-se ao arquivo sem as modificações, ideal para praticar o passo a passo e treinar suas habilidades. O arquivo pronto é o arquivo final, com todas as modificações ensinadas já aplicadas, ideal se você já quiser ter em mãos o resultado.
Para baixar os arquivos, acesse a página de download e clique no botão Baixar.
Versão em texto / ilustrada
Calculando a média ponderada
Observe o exemplo a seguir. Há uma nota para cada atividade, mas também um peso. Na célula F2 é possível observar a média aritmética comum das notas (8,25). No entanto, não podemos dar a uma nota de peso 5% a mesma importância de uma nota de peso 20%, por exemplo. Nesse caso, precisamos da média ponderada.
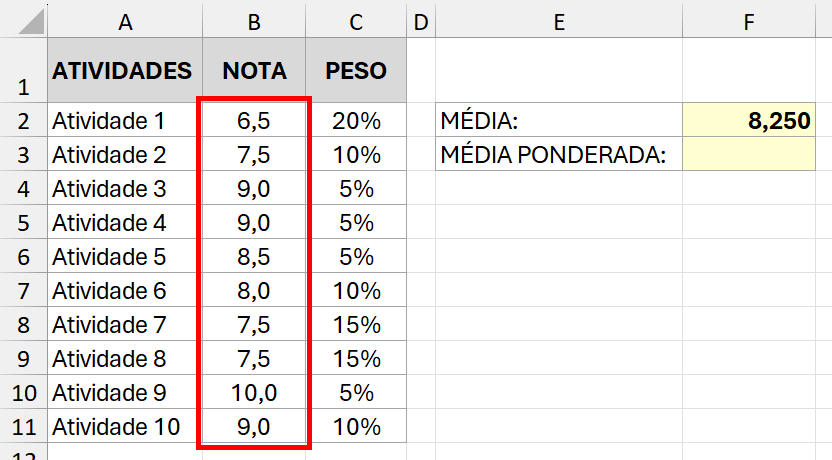
A média ponderada funciona basicamente com o mesmo princípio da média aritmética comum, mas, nesse caso, cada nota deve ser multiplicada por seu respectivo peso. Para isso, podemos fazer uso da função SOMARPRODUTO, que multiplica os valores em linha e soma todos os produtos calculados.
=SOMARPRODUTO(B2:B11;C2:C11)
Em seguida, dividimos esse valor pela soma dos pesos:
=SOMARPRODUTO(B2:B11;C2:C11)/SOMA(C2:C11)

Observe a diferença de valores. A média ponderada é menor porque leva em consideração o peso das notas. Uma nota menor em uma atividade com maior peso é mais relevante que uma nota maior em uma atividade com menor peso.
Agora observe este outro exemplo. Vamos calcular a média salarial de uma empresa. Não basta apenas calcular a média dos valores salariais únicos, porque há quantidades diferentes de funcionários recebendo determinado salário. É um ótimo exemplo de uso da média ponderada.
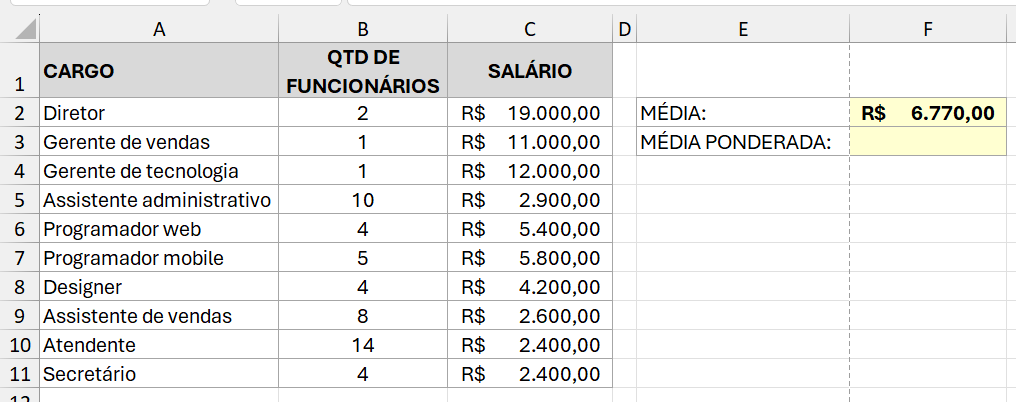
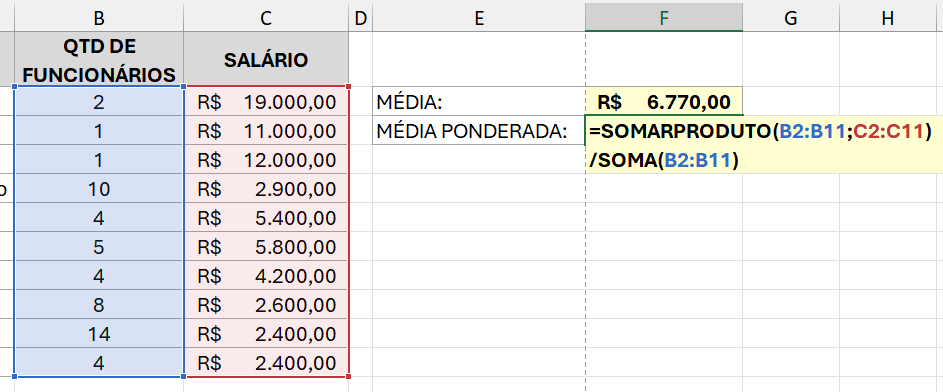
Observe que o mesmo princípio se aplica: é mais relevante o peso de 14 salários de R$ 2.400,00 do que 1 único salário de R$ 11.000,00, por exemplo. Dessa forma, há uma divergência significativa entre as médias comum e ponderada.

Dicas e informações complementares
- A divisão deve ser sempre realizada pela soma dos pesos, nunca pela soma dos valores.